|
|
| (同じ利用者による、間の6版が非表示) |
| 1行目: |
1行目: |
| − | {{要改訳}}
| |
| − | {{正確性|date=2015年2月}}
| |
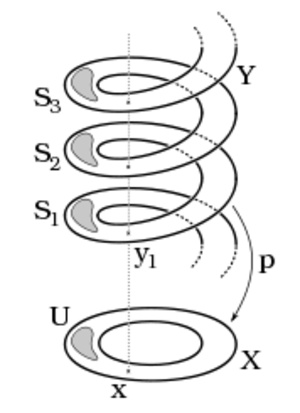
| | [[File:Covering map.svg|thumb|被覆写像 p : Y → X によって底空間 X の開集合 U は被覆空間 Y の同相な開集合 S<sub>1</sub>, S<sub>2</sub>, S<sub>3</sub>, … によって「均一に被覆」されている。]] | | [[File:Covering map.svg|thumb|被覆写像 p : Y → X によって底空間 X の開集合 U は被覆空間 Y の同相な開集合 S<sub>1</sub>, S<sub>2</sub>, S<sub>3</sub>, … によって「均一に被覆」されている。]] |
| − | 数学、特に[[代数的位相幾何学|代数トポロジー]]において、'''被覆写像'''(covering map)あるいは'''被覆射影'''(covering projection)とは、[[位相空間]] C から X への[[連続写像|連続]][[全射]] p のうち、 X の各点が p により「均一に被覆される」[[開集合|開]][[近傍]]をもつものをいう。厳密な定義は追って与える。このとき C を'''被覆空間'''(covering space)、X を'''底空間'''(base space)と呼ぶ。この定義は、すべての被覆写像は[[局所同相]]であることを意味する。
| + | '''被覆写像'''(covering map)あるいは'''被覆射影'''(covering projection) |
| | | | |
| − | 被覆空間は[[ホモトピー論]]、[[調和解析]]、[[リーマン幾何学]]、[[微分幾何学]]で重要な役割を果たす。たとえば、リーマン幾何学では、[[分岐 (数学)#代数トポロジーでは|分岐]]は、被覆写像の考え方の一般化である。また、被覆写像は[[ホモトピー群]]、特に[[基本群]]の研究とも深く関係する: X が十分によい位相空間であれば、X の被覆の同値類の集合と [[基本群]] π<sub>1</sub>(X) の共役な部分群の類全体との間に[[全単射]]が存在する(被覆の分類定理){{sfn|Bredon|1993|loc={{google books quote|id=G74V6UzL_PUC|page=154|Theorem 8.1}}}}。
| + | [[リーマン面]]のときのように,空間 <i>X</i> を何重かに重ねて考える必要のあるとき,その重なったもの [[ファイル:09788800 siki1.gif]] |
| − | <!--{{refimprove|date=June 2012}}
| + | をつくり,射影 [[ファイル:09788800 siki2.gif|フレームなし]] で考える。この [[ファイル:09788800 siki1.gif]]を <i>X</i> の被覆空間という。 |
| − | | |
| − | [[File:Covering space diagram.svg|thumb|250px|right|A covering map satisfies the local triviality condition. Intuitively, such maps locally project a "stack of pancakes" above an [[open set|open region]], ''U'', onto ''U''.]]
| |
| − | | |
| − | In [[mathematics]], more specifically [[algebraic topology]], a '''covering map''' (also '''covering projection''') is a [[continuous function|continuous]] [[Function (mathematics)|function]] ''p'' <ref>{{cite book |last=Spanier |first=Edwin |title=Algebraic Topology |year=1966 |publisher=McGraw-Hill |page=62|isbn=}}</ref> from a [[topological space]], ''C'', to a topological space, ''X'', such that each point in ''X'' has an [[open set|open]] neighbourhood '''evenly covered''' by ''p'' (as shown in the image); the precise definition is given below. In this case, ''C'' is called a '''covering space''' and ''X'' the '''base space''' of the covering projection. The definition implies that every covering map is a [[local homeomorphism]].
| |
| − | | |
| − | Covering spaces play an important role in [[homotopy theory]], [[harmonic analysis]], [[Riemannian geometry]] and [[differential topology]]. In Riemannian geometry for example, [[Ramification#In algebraic topology|ramification]] is a generalization of the notion of covering maps. Covering spaces are also deeply intertwined with the study of homotopy groups and, in particular, the [[fundamental group]]. An important application comes from the result that, if ''X'' is a "sufficiently good" [[topological space]], there is a [[bijection]] from the collection of all isomorphism classes of [[connected space|connected coverings]] of ''X'' and subgroups of the [[fundamental group]] of ''X''.-->
| |
| − | | |
| − | == 定義 ==
| |
| − | [[位相空間]] C から X への[[連続写像|連続]][[全射]] p : C → X が'''被覆写像'''であるとは、すべての点 x ∈ X に対し x の開近傍 U が存在し、逆像 p<sup>−1</sup>(U) が共通部分をもたない C の開集合の和集合で表され、各開集合が p の制限写像により U と同相であることをいう{{sfn|Munkres|2000|p=336}}。このとき C を'''被覆空間'''、 X を'''底空間'''という。被覆写像や被覆空間のことを単に被覆と呼ぶこともある。
| |
| − | | |
| − | 底空間の点 x における逆像 p<sup>−1</sup>(x) は x 上の[[ファイバー]]と呼ばれ、[[離散空間]]となる{{sfn|Munkres|2000|p=336}}。
| |
| − | | |
| − | 定義中に現れる点 x の特別な開近傍 U は、'''均一被覆近傍'''{{訳語疑問点|date=2016-08-07}}<!-- evenly cover*ed* neighborhoods 直訳すればむしろ均一*被*被覆近傍だがこれも言い難い -->と言う。均一被覆近傍は、空間 X の[[開被覆]]となる。均一被覆近傍 U の C における同相なコピーを、U 上の'''シート'''と言う。一般に図示するときには、被覆空間 C は底空間 X 上に「浮いて」いて、 p が「下向き」に写像し、U 上のシートは、U の「真上方向に水平に積み重なって」いて、x 上のファイバーは、x の「真上」にある C の点であることが多い。特に、被覆写像は局所的には自明である。このことは局所的には、均一被覆近傍 U の前像 p<sup>−1</sup>(U) の U × F の上への準同型 h が、各々の被覆写像が射影と同型であることを意味する。ここに F はファイバーであり、'''局所自明化条件'''、つまり、U の上への U × F から U の上への射影 π : U × F → U に対して、射影 π と準同型 h との合成は、前像 p<sup>−1</sup>(U) から U 上への写像 π ∘ h であり、従って、導かれた合成 π ∘ h は p に局所的に(p<sup>−1</sup>(U) の中では)等しい。
| |
| − | <!--== Formal definition ==Let ''X'' be a [[topological space]]. A '''covering space''' of ''X'' is a space ''C'' together with a [[continuous function (topology)|continuous]] [[surjective]] map
| |
| − | | |
| − | :<math>p \colon C \to X\,</math>
| |
| − | | |
| − | such that for every {{nowrap|''x'' ∈ ''X''}}, there exists an [[open set|open]] [[neighborhood (topology)|neighborhood]] ''U'' of ''x'', such that ''p''<sup>−1</sup>(''U'') (the [[inverse image]] of ''U'' under ''p'') is a union of disjoint open sets in ''C'', each of which is mapped [[homeomorphism|homeomorphically]] onto ''U'' by ''p''.<ref name="Chernavskii">{{harvnb|Chernavskii|2001}}</ref><ref name="Munkres p336">{{harvnb|Munkres|2000|p=336}}</ref>
| |
| − | | |
| − | The map ''p'' is called the '''covering map''',<ref name="Munkres p336"/> the space ''X'' is often called the '''base space''' of the covering, and the space ''C'' is called the '''total space''' of the covering. For any point ''x'' in the base the inverse image of ''x'' in ''C'' is necessarily a [[discrete space]]<ref name="Munkres p336"/> called the [[Fiber (mathematics)|fiber]] over ''x''.
| |
| − | | |
| − | The special open neighborhoods ''U'' of ''x'' given in the definition are called '''evenly-covered neighborhoods'''. The evenly-covered neighborhoods form an [[open cover]] of the space ''X''. The homeomorphic copies in ''C'' of an evenly-covered neighborhood ''U'' are called the '''sheets''' over ''U''. One generally pictures ''C'' as "hovering above" ''X'', with ''p'' mapping "downwards", the sheets over ''U'' being horizontally stacked above each other and above ''U'', and the fiber over ''x'' consisting of those points of ''C'' that lie "vertically above" ''x''. In particular, covering maps are locally trivial. This means that locally, each covering map is 'isomorphic' to a projection in the sense that there is a homeomorphism, ''h'', from the pre-image ''p''<sup>−1</sup>(''U''), of an evenly covered neighbourhood ''U'', onto {{nowrap|''U'' × ''F''}}, where ''F'' is the fiber, satisfying the '''local trivialization condition''', which is that, if we project {{nowrap|''U'' × ''F''}} onto ''U'', {{nowrap|''π'' : ''U'' × ''F'' → ''U''}}, so the composition of the projection ''π'' with the homeomorphism ''h'' will be a map {{nowrap|''π'' ∘ ''h''}} from the pre-image ''p''<sup>−1</sup>(''U'') onto ''U'', then the derived composition {{nowrap|''π'' ∘ ''h''}} will equal ''p'' locally (within ''p''<sup>−1</sup>(''U'')).-->
| |
| − | | |
| − | ===他の定義===
| |
| − | 被覆写像の定義では位相空間 C と X にある種の連結性を課すこともある。特に[[弧状連結]]や[[局所弧状連結]]を要請することが多い{{sfn|Lickorish|1997|loc={{google books quote|id=PhHhw_kRvewC|page=66|Definition 7.1}}}}{{sfn|Bredon|1993|loc={{google books quote|id=G74V6UzL_PUC|page=139|Definition 3.1}}}}。実際、多くの定理はこれらの条件の下でしか成り立たない。被覆写像の全射性を要請しない場合もあるが、もし C が弧状連結で空でないならば全射性は他の公理から従う。
| |
| − | <!--===Alternative definitions===
| |
| − | Many authors impose some [[connectedness|connectivity]] conditions on the spaces ''X'' and ''C'' in the definition of a covering map. In particular, many authors require both spaces to be [[path-connected]] and [[locally path-connected]].<ref>{{Cite book|title = An Introduction to Knot Theory|date = 1997|last = Lickorish|pages = 66–67}}</ref><ref>{{Cite book|title = Topology and Geometry|last = Bredon|year = 1997|isbn = 978-0387979267}}</ref> This can prove helpful because many theorems hold only if the spaces in question have these properties. Some authors omit the assumption of surjectivity, for if ''X'' is connected and ''C'' is nonempty then surjectivity of the covering map actually follows from the other axioms.-->
| |
| − | | |
| − | == 具体例 ==
| |
| − | * すべての位相空間は恒等写像によって自明に自分自身を被覆する。
| |
| − | | |
| − | [[File:DoubleCoveredCircle.svg|thumb|100px|S<sup>1</sup> は S<sup>1</sup> の二重被覆である。]]
| |
| − | * 複素平面上の単位円を S<sup>1</sup> と書く。すると、
| |
| − | ::p(z) = z<sup>n</sup>
| |
| − | :により、写像 p : S<sup>1</sup> → S<sup>1</sup> は n 重被覆となる。
| |
| − | | |
| − | * <math>\mathbb{R}</math> は、単位円 S<sup>1</sup> の普遍被覆である。指数写像
| |
| − | ::p(t) = exp(2πit)
| |
| − | :により、写像 p : '''R''' → S<sup>1</sup> は被覆で、S<sup>1</sup> の各点は無限回被覆される。
| |
| − | | |
| − | * 位相空間 X が[[普遍被覆]]を持つことは、連結かつ局所弧状連結かつ[[半局所単連結]]であることと同値である。
| |
| − | | |
| − | * [[スピン群]] Spin(n) は[[特殊直交群]]の二重被覆であり、n > 2 のときは普遍被覆である。従って、リー群の{{仮リンク|例外同型|en|exceptional isomorphism}}(exceptional isomorphism)は、低次元のスピン群と古典リー群の間の同型を与える。
| |
| − | | |
| − | * [[ユニタリ群]] U(n) は普遍被覆 SU(n) × R を持つ。
| |
| − | | |
| − | * [[n-次元球面]] S<sup>n</sup> は、実射影空間の二重被覆であり、n > 1 の場合は普遍被覆である。
| |
| − | | |
| − | * すべての多様体は、連結であることと向き付け不能であることが同値であるような[[向き付け可能性#向き付け可能二重被覆|向き付け可能二重被覆]]を持っている。
| |
| − | | |
| − | * [[一意化定理]]は、すべての単連結なリーマン面は[[リーマン球面]]、複素平面、単位円板に[[共形同値]]であるという定理である。
| |
| − | | |
| − | * n 個の円のウェッジの普遍被覆は、n 個の生成子を持つ自由群の[[ケイリーグラフ]](Cayley graph)である、つまり、[[ベーテ格子]]である。
| |
| − | | |
| − | * [[トーラス]]は[[クラインの壷]]の二重被覆である。
| |
| − | | |
| − | * すべてのグラフは、{{仮リンク|二つ折りの二重被覆|en|bipartite double cover}}(bipartite double cover)である。すべてのグラフは円のウェッジとホモトピー同値であるので、普遍被覆はケイレーグラフとなる。
| |
| − | | |
| − | * コンパクト多様体の同一次元の多様体への埋め込みは、いつも埋め込みの像の被覆である。
| |
| − | <!--== Examples ==
| |
| − | * Every space trivially covers itself.
| |
| − | | |
| − | * A topological space ''X'' has a [[universal cover]] if and only if it is connected, locally path connected, and [[semi-locally simply connected]].
| |
| − | | |
| − | * <math>\mathbb{R}</math> is the universal cover of the unit circle ''S<sup>1</sup>''
| |
| − | | |
| − | * The [[spin group]] ''Spin(n)'' is a double cover of the [[special orthogonal group]] and a universal cover when ''n > 2''. The accidental, or [[exceptional isomorphism]]s for Lie groups then give isomorphisms between spin groups in low dimension and classical Lie groups.
| |
| − | | |
| − | * The [[unitary group]] ''U(n)'' has universal cover ''SU(n) x R''
| |
| − | | |
| − | * The [[n-sphere]] ''S<sup>n</sup>'' is a double cover of real projective space ''RP<sup>n</sup>'' and is a universal cover for ''n >1''.
| |
| − | | |
| − | * Every manifold has an [[orientable double cover]] that is connected if and only if the manifold is non-orientable.
| |
| − | | |
| − | * The [[uniformization theorem]] asserts that every simply connected Riemann surface has a universal cover conformally equivalent to the [[Riemann sphere]], the complex plane, or the unit disc.
| |
| − | | |
| − | * The universal cover of a wedge of ''n'' circles is the [[Cayley graph]] of the free group on ''n'' generators, i.e. a [[Bethe lattice]].
| |
| − | | |
| − | * The [[torus]] is a double cover of the [[Klein bottle]]
| |
| − | | |
| − | * Every graph has a [[bipartite double cover]]. Since every graph is homotopic to a wedge of circles, its universal cover is a Cayley graph.
| |
| − | | |
| − | * Every immersion from a compact manifold to a manifold of the same dimension is a covering of its image.-->
| |
| − | * 有限群のアーベル的な無限分岐被覆グラフは、結晶構造の抽象化したものとみなすことができる<ref>[[砂田利一| Sunada T.]] (2012), ''Topological Crystallography ---With a View Towards Discrete Geometric Analysis---", Surveys and Tutorials in the Applied Mathematical Sciences, Vol. 6, Springer </ref>。たとえば、抽象グラフとしての{{仮リンク|ダイアモンドの結晶構造|en|diamond cubic}}(diamond crystal)は、{{仮リンク|ダイポールグラフ|en|dipole graph}}(dipole graph) D<sub>4</sub> のアーベル的最大被覆グラフである。
| |
| − | <!--* Infinite-fold abelian covering graphs of finite graphs are regarded as abstractions of crystal structures. <ref>[[Toshikazu Sunada| Sunada T.]] (2012), ''Topological Crystallography ---With a View Towards Discrete Geometric Analysis---", Surveys and Tutorials in the Applied Mathematical Sciences, Vol. 6, Springer </ref> For instance the [[diamond cubic|diamond crystal]] as an abstarct graph is the maximal abelian covering graph of the [[dipole graph]] D<sub>4</sub>-->
| |
| − | | |
| − | == 性質 ==
| |
| − | | |
| − | ===共通な局所的性質===
| |
| − | * 任意の被覆 p : C → X は[[局所同相]]である{{sfn|Munkres|2000|p=338}}、つまり、すべての c ∈ C に対し、c の近傍 U ⊆ C と p(c) の近傍 V ⊆ X が存在し、U への p の制限が U から V への[[同相]]となっている。このことは、C と X がすべての局所的性質を共有していることを意味する。X が[[単連結]]で C が連結であれば、このことは大域的にも同じく成立して、被覆 p は同相である。
| |
| − | * p : E → B と p' : E' → B' が被覆写像であれば、(p × p')(e, e') = (p(e), p'(e')) により与えられる写像 p × p' : E × E' → B × B' も被覆写像である{{sfn|Munkres|2000|p=339|loc=Theorem 53.3}}。
| |
| − | <!--== Properties ==
| |
| − | | |
| − | ===Common local properties===
| |
| − | * Every cover {{nowrap|''p'': ''C'' → ''X''}} is a [[local homeomorphism]]<ref>{{harvnb|Munkres|2000|p=338}}</ref>—that is, for every {{nowrap|''c'' ∈ ''C''}}, there exists a neighborhood {{nowrap|''U'' ⊆ ''C''}} of ''c'' and a neighborhood {{nowrap|''V'' ⊆ ''X''}} of ''p''(''c'') such that the restriction of ''p'' to ''U'' yields a [[homeomorphism]] from ''U'' to ''V''. This implies that ''C'' and ''X'' share all local properties. If ''X'' is [[simply connected]] and ''C'' is connected, then this holds globally as well, and the covering ''p'' is a homeomorphism.
| |
| − | * If {{nowrap|''p'' : ''E'' → ''B''}} and {{nowrap|''p''′ : ''E''′ → ''B''′}} are covering maps, then so is the map {{nowrap|''p'' × ''p''′ : ''E'' × ''E''′ → ''B'' × ''B′''}} given by {{nowrap|1=(''p'' × ''p''′)(''e'', ''e''′) = (''p''(''e''), ''p''′(''e''′))}}.<ref>{{harvnb|Munkres|2000|p=339|loc=Theorem 53.3}}</ref>-->
| |
| − | | |
| − | ===ファイバーの準同型===
| |
| − | すべての x ∈ X に対し、x 上のファイバーは C の離散部分集合である{{sfn|Munkres|2000|p=336}}。X 上の[[連結空間|連結成分]]上で、ファイバーは準同型である。
| |
| − | | |
| − | X 連結であれば、離散空間 F が存在し、すべての x ∈ X に対し、x 上のファイバーは F に[[準同型]]であり、さらにすべての x ∈ X に対し、x の近傍 U が存在し、その全前イメージ p<sup>−1</sup>(U) は U × F と同相である。特に、x 上のファイバーの数値密度(点の数)は、F の点の数に等しく、被覆写像 p : C → X の'''次数'''と呼ぶ。このように、すべてのファイバーが n 個の元を持つと、'''n-重の被覆'''と呼ぶ(n = 1 のときは自明な被覆といい、n = 2 のときは'''二重被覆'''といい、n = 3 のときは'''三重被覆'''と言う)。
| |
| − | <!--===Homeomorphism of the fibres===
| |
| − | For every ''x'' in ''X'', the fiber over ''x'' is a [[discrete space|discrete]] subset of ''C''.<ref name="Munkres p336"/> On every [[connected space|connected component]] of ''X'', the fibers are homeomorphic.
| |
| − | | |
| − | If ''X'' is connected, there is a discrete space ''F'' such that for every ''x'' in ''X'' the fiber over ''x'' is [[homeomorphism|homeomorphic]] to ''F'' and, moreover, for every ''x'' in ''X'' there is a neighborhood ''U'' of ''x'' such that its full pre-image ''p''<sup>−1</sup>(''U'') is homeomorphic to {{nowrap|''U'' × ''F''}}. In particular, the [[cardinality]] of the fiber over ''x'' is equal to the cardinality of ''F'' and it is called the '''degree of the cover''' {{nowrap|''p'' : ''C'' → ''X''}}. Thus, if every fiber has ''n'' elements, we speak of an '''''n''-fold covering''' (for the case {{nowrap|1=''n'' = 1}}, the covering is trivial; when {{nowrap|1=''n'' = 2}}, the covering is a '''double cover'''; when {{nowrap|1=''n'' = 3}}, the covering is a '''triple cover''' and so on).-->
| |
| − | | |
| − | ===持ち上げ===
| |
| − | {{see also|{{仮リンク|ホモトピーリフトの性質|en|Homotopy lifting property}}(Homotopy lifting property) }}
| |
| − | | |
| − | p : C → X が被覆で γ が X 内の経路(つまり、単位区間 [0,1] から X の中への連続写像)であり、c ∈ C が γ(0) の上の点(つまり、p(c) = γ(0))ならば、γ 上の C のある経路 ρ (つまり、p o ρ = γ)が一意に存在し、ρ(0) = c である。ρ は、γ の'''持ち上げ'''(あるいは、'''リフト''')と呼ぶ。x と y が X の連結な経路で結ばれている場合、この経路は、持ち上げの性質を通して、x 上のファイバーと y 上のファイバーの間の全単射を与える。
| |
| − | <!--===Lifting properties===
| |
| − | {{see also|Homotopy lifting property}}
| |
| − | If {{nowrap|1=''p'' : ''C'' → ''X''}} is a cover and γ is a path in ''X'' (i.e. a continuous map from the [[unit interval]] {{nowrap|[0, 1]}} into ''X'') and {{nowrap|''c'' ∈ ''C''}} is a point "lying over" γ(0) (i.e. {{nowrap|1=''p''(''c'') = γ(0))}}, then there exists a unique path Γ in ''C'' lying over γ (i.e. {{nowrap|1=''p'' ∘ Γ = γ}}) such that with {{nowrap|1=Γ(0) = ''c''}}. The curve Γ is called the '''lift''' of γ. If ''x'' and ''y'' are two points in ''X'' connected by a path, then that path furnishes a [[bijection]] between the fiber over ''x'' and the fiber over ''y'' via the lifting property.-->
| |
| − | | |
| − | さらに一般的には、f : Z → X を [[弧状連結]]で[[局所弧状連結]]な空間 Z への X からの連続写像として、基点 z ∈ Z を固定し、f(z) の'''上にある'''点 c ∈ C(つまり、p(c) = f(z))をとる。このとき、f の'''持ち上げ'''(つまり、連続写像 g : Z → C であって、p ∘ g = f, g(z) = c を満たす)が存在することは、[[基本群]]の間の{{仮リンク|誘導準同型|en|induced homomorphism}}(induced homomorphism) f<sub>#</sub> : π<sub>1</sub>(Z, z) → π<sub>1</sub>(X, f(z)) と p<sub>#</sub> : π<sub>1</sub>(C, c) → π<sub>1</sub>(X, f(z)) が、
| |
| − | | |
| − | {{NumBlk|::|<math>f_\#(\pi_1(Z,z))\subset p_\#(\pi_1(C,c)). </math>|{{EquationRef|♠}}}}
| |
| − | | |
| − | を満たすことと同値である。
| |
| − | | |
| − | さらに、そのような f の持ち上げ g が存在する場合は、一意的である。
| |
| − | <!--More generally, let {{nowrap|''f'' : ''Z'' → ''X''}} be a continuous map to ''X'' from a [[path connected]] and [[locally path connected]] space ''Z''. Fix a base-point {{nowrap|''z'' ∈ ''Z''}}, and choose a point {{nowrap|''c'' ∈ ''C''}} "lying over" ''f''(''z'') (i.e. {{nowrap|1=''p''(''c'') = ''f''(''z'')}}). Then there exists a '''lift''' of ''f'' (that is, a continuous map {{nowrap|''g'' : ''Z'' → ''C''}} for which {{nowrap|1=''p'' ∘ ''g'' = ''f''}} and {{nowrap|1=''g''(''z'') = ''c''}}) [[if and only if]] the [[induced homomorphism]]s {{nowrap|''f''<sub>#</sub> : π<sub>1</sub>(''Z'', ''z'') → π<sub>1</sub>(''X'', ''f''(''z''))}} and {{nowrap|''p''<sub>#</sub> : π<sub>1</sub>(''C'', ''c'') → π<sub>1</sub>(''X'', ''f''(''z''))}} at the level of [[fundamental groups]] satisfy
| |
| − | | |
| − | {{NumBlk|::|<math>f_\#(\pi_1(Z,z))\subset p_\#(\pi_1(C,c)). </math>|{{EquationRef|♠}}}}
| |
| − | | |
| − | Moreover, if such a lift ''g'' of ''f'' exists, it is unique.-->
| |
| − | <!--In particular, if the space ''Z'' is assumed to be [[simply connected]] (so that {{nowrap|π<sub>1</sub>(''Z'', ''z'')}} is trivial), condition {{EquationNote|♠|(♠)}} is automatically satisfied, and every continuous map from ''Z'' to ''X'' can be lifted. Since the unit interval {{nowrap|[0, 1]}} is simply connected, the lifting property for paths is a special case of the lifting property for maps stated above.
| |
| − | | |
| − | If {{nowrap|''p'' : ''C'' → ''X''}} is a covering and {{nowrap|''c'' ∈ ''C''}} and {{nowrap|''x'' ∈ ''X''}} are such that {{nowrap|1=''p''(''c'') = ''x''}}, then ''p''<sub>#</sub> is injective at the level of [[fundamental groups]], and the induced homomorphisms {{nowrap|''p''<sub>#</sub> : π<sub>''n''</sub>(''C'', ''c'') → π<sub>''n''</sub>(''X'', ''x'')}} are [[group isomorphism|isomorphisms]] for all {{nowrap|''n'' ≥ 2}}. Both of these statements can be deduced from the lifting property for continuous maps. Surjectivity of ''p''<sub>#</sub> for {{nowrap|''n'' ≥ 2}} follows from the fact that for all such ''n'', the ''n''-sphere '''S'''<sup>''n''</sup> is simply connected and hence every continuous map from '''S'''<sup>''n''</sup> to ''X'' can be lifted to ''C''.-->
| |
| − | | |
| − | ===同値性===
| |
| − | p<sub>1</sub> : C<sub>1</sub> → X と p<sub>2</sub> : C<sub>2</sub> → X が 2 つの被覆だとする。
| |
| − | (p<sub>1</sub>, C<sub>1</sub>) と (p<sub>2</sub>, C<sub>2</sub>) は、ある同相写像 p<sub>21</sub> : C<sub>2</sub> → C<sub>1</sub> が存在し、p<sub>2</sub> = p<sub>1</sub>op<sub>21</sub> のとき、同値であると言う。これは同値関係である。被覆の同値類は、共役類に対応する。p<sub>21</sub> が同相写像でなく被覆の場合には、
| |
| − | (p<sub>2</sub>, C<sub>2</sub>) は (p<sub>1</sub>, C<sub>1</sub>) を'''支配する'''(dominate)と言う。ここに、p<sub>2</sub> = p<sub>1</sub>op<sub>21</sub> である。
| |
| − | <!--===Equivalence===
| |
| − | Let {{nowrap|''p''<sub>1</sub> : ''C''<sub>1</sub> → ''X''}} and {{nowrap|''p''<sub>2</sub> : ''C''<sub>2</sub> → ''X''}} be two coverings. One says that the two coverings ''p''<sub>1</sub> and ''p''<sub>2</sub> are '''equivalent''' if there exists a homeomorphism {{nowrap|''p''<sub>21</sub> : ''C''<sub>2</sub> → ''C''<sub>1</sub>}} and such that {{nowrap|1=''p''<sub>2</sub> = ''p''<sub>1</sub> ∘ ''p''<sub>21</sub>}}. Equivalence classes of coverings correspond to conjugacy classes of subgroups of the [[fundamental group]] of ''X'', as discussed below. If {{nowrap|''p''<sub>21</sub> : ''C''<sub>2</sub> → ''C''<sub>1</sub>}} is a covering (rather than a homeomorphism) and {{nowrap|1=''p''<sub>2</sub> = ''p''<sub>1</sub> ∘ ''p''<sub>21</sub>}}, then one says that ''p''<sub>2</sub> '''dominates''' ''p''<sub>1</sub>.-->
| |
| − | | |
| − | ===多様体の被覆===
| |
| − | 被覆は局所[[同相]]であるので、n-次元[[多様体#位相多様体|位相多様体]]の被覆は n-次元多様体である。(被覆空間が[[第二可算空間|第二可算]]であることは、多様体の[[基本群]]がいつも[[可算]]であるという事実より証明することができる。)しかし、n-次元多様体で覆われた空間は、[[ハウスドルフ空間|非ハウスドルフ空間]]かもしれない。例えば、C を原点を取り去った平面とし、X を全ての点 {{nowrap|(x, y)}} を {{nowrap|(2x, y/2)}} で同一視する。{{nowrap|p : C → X}} が商写像とすると、{{nowrap|1=f(x, y) = (2x, y/2)}} で生成される C への Z の作用は{{仮リンク|固有不連続|en|properly discontinuous}}(properly discontinuous)であるので、被覆である。点 {{nowrap|p(1, 0)}} と {{nowrap|p(0, 1)}} は X の中では切り離されるような近傍を持たない。
| |
| − | | |
| − | 微分可能多様体の任意の被覆空間は、p (問題の被覆写像)を[[局所微分同相]]、つまり、{{仮リンク|ランク (微分トポロジー)|label=ランク|en|Rank (differential topology)}}(rank)へ変えるような自然な微分構造を持っているかもしれない。
| |
| − | <!--===Covering of a manifold===
| |
| − | Since coverings are local [[homeomorphism]]s, a covering of a topological ''n''-[[manifold]] is an ''n''-manifold. (One can prove that the covering space is [[second-countable]] from the fact that the [[fundamental group]] of a manifold is always [[countable]].) However a space covered by an ''n''-manifold may be a [[non-Hausdorff manifold]]. An example is given by letting ''C'' be the plane with the origin deleted and ''X'' the quotient space obtained by identifying every point {{nowrap|(''x'', ''y'')}} with {{nowrap|(2''x'', ''y''/2)}}. If {{nowrap|''p'' : ''C'' → ''X''}} is the quotient map then it is a covering since the action of ''Z'' on ''C'' generated by {{nowrap|1=''f''(''x'', ''y'') = (2''x'', ''y''/2)}} is [[properly discontinuous]]. The points {{nowrap|''p''(1, 0)}} and {{nowrap|''p''(0, 1)}} do not have disjoint neighborhoods in ''X''.
| |
| − | | |
| − | Any covering space of a differentiable manifold may be equipped with a (natural) differentiable structure that turns ''p'' (the covering map in question) into a [[local diffeomorphism]] – a map with constant [[Rank (differential topology)|rank]] ''n''.-->
| |
| − | | |
| − | == 普遍被覆 ==
| |
| − | 連結な被覆空間が[[単連結空間|単連結]]のとき、'''普遍被覆'''(universal cover)という。普遍被覆の名称は、以下の[[普遍性]]という重要な性質に由来する。写像 q : D → X を X の普遍被覆とし、写像 p : C → X を X の任意の被覆とし、さらに、被覆空間 C が連結とすると、被覆写像 f : D → C が存在し、p o f = q となる。このことは、
| |
| − | | |
| − | :「X の普遍被覆は、すべての X の連結な被覆を被覆する」
| |
| − | | |
| − | と言うことができる。
| |
| − | | |
| − | 写像 f は、以下の意味で一意的である。x ∈ X を固定し、d ∈ D に対し q (d) = x で、c ∈ C に対し p (c) = x とすると、一意な被覆写像 f : D → C が存在し、p o f = q、かつ f (d) = c となる。
| |
| − | <!--== Universal covers ==
| |
| − | A covering space is a '''universal covering space''' if it is [[simply connected]]. The name ''[[universal property|universal]] cover'' comes from the following important property: if the mapping {{nowrap|''q'': ''D'' → ''X''}} is a universal cover of the space ''X'' and the mapping {{nowrap|''p'' : ''C'' → ''X''}} is any cover of the space ''X'' where the covering space ''C'' is connected, then there exists a covering map {{nowrap|''f'' : ''D'' → ''C''}} such that {{nowrap|1=''p'' ∘ ''f'' = ''q''}}. This can be phrased as
| |
| − | | |
| − | <BLOCKQUOTE >The universal cover of the space ''X'' covers all connected covers of the space ''X''.</BLOCKQUOTE >
| |
| − | | |
| − | The map ''f'' is unique in the following sense: if we fix a point ''x'' in the space ''X'' and a point ''d'' in the space ''D'' with {{nowrap|1=''q''(''d'') = ''x''}} and a point ''c'' in the space ''C'' with {{nowrap|1=''p''(''c'') = ''x''}}, then there exists a unique covering map {{nowrap|''f'' : ''D'' → ''C''}} such that {{nowrap|1=''p'' ∘ ''f''= ''q''}} and {{nowrap|1=''f''(''d'') = ''c''}}.-->
| |
| − | | |
| − | X が普遍被覆をもつならば、普遍被覆は本質的に一意である。q<sub>1</sub> : D<sub>1</sub> → X と q<sub>2</sub> : D<sub>2</sub> → X が X の 2つの普遍被覆とすると、同相写像 f : D<sub>1</sub> → D<sub>2</sub> が存在し、q<sub>2</sub> o f = q<sub>1</sub> となる。
| |
| − | | |
| − | 空間 X が、[[連結空間#弧状連結|弧状連結]]で、[[連結空間#局所連結性|局所弧状連結]]であり、[[半局所単連結]]であるとき、そのときに限り、普遍被覆を持つ。X の普遍被覆は、X の経路の空間から構成することができる。
| |
| − | <!--If the space ''X'' has a universal cover then that universal cover is essentially unique: if the mappings {{nowrap|''q''<sub>1</sub> : ''D''<sub>1</sub> → ''X''}} and {{nowrap|''q''<sub>2</sub> : ''D''<sub>2</sub> → ''X''}} are two universal covers of the space ''X'' then there exists a homeomorphism {{nowrap|''f'' : ''D''<sub>1</sub> → ''D''<sub>2</sub>}} such that {{nowrap|1=''q''<sub>2</sub> ∘ ''f'' = ''q''<sub>1</sub>}}.
| |
| − | | |
| − | The space ''X'' has a universal cover if it is [[Connected space|connected]], [[Connected space#Local connectedness|locally path-connected]] and [[semi-locally simply connected]]. The universal cover of the space ''X'' can be constructed as a certain space of paths in the space ''X''.-->
| |
| − | | |
| − | 上に示した '''R''' → '''S'''<sup>1</sup> は普遍被覆の例である。{{仮リンク|四元数と空間回転|en|quaternions and spatial rotation}}(quaternions and spatial rotation)に示されている[[四元数]]から三次元[[回転群]]への写像 '''S'''<sup>3</sup> → SO(3) も、普遍被覆である。
| |
| − | | |
| − | X がさらに別な構造をもつ場合、普遍被覆も、通常その構造を引き継ぐ。
| |
| − | * X が[[多様体]]ならば、普遍被覆 D も多様体である。
| |
| − | * X が[[リーマン面]]ならば、普遍被覆 D もリーマン面で、p は[[正則]]写像である。
| |
| − | * X が[[擬リーマン多様体#ローレンツ多様体|ローレンツ多様体]](つまり、符号数 (p,1) の計量を有する擬リーマン多様体)ならば、普遍被覆 D もローレンツ多様体である。さらに、p<sup>−1</sup>(U) を、共通部分をもたない開集合の和集合で、各々の開集合が p により U と可微分同相とする。X が時間的(timelike)閉曲線を含むとき、X は時間的複連結である(いかなる時間的閉曲線も、任意の点と時間的にホモトープとなることができず、どの点も因果的に上手く振舞えないからである)。従って、そのような空間の(可微分)普遍被覆は{{仮リンク|時間的単連結|en|timelike simply connected}}(timelike simply connected)である(時間的閉曲線を含まない)。
| |
| − | * X が[[リー群]]ならば(上記二つの例と同様)、D もリー群であり、p はリー群の準同型である。この場合、普遍被覆は'''普遍被覆群'''とも呼ばれる。普遍被覆群は、[[表現論]]と[[量子力学]]に重要な応用を持つ。普遍被覆群の通常の群表現 (D) は、元の(古典)群の{{仮リンク|射影表現|en|projective representation}}(projective representation) (X) だからである。
| |
| − | | |
| − | 普遍被覆は、[[解析接続]]が自然にできる領域として、[[解析函数]]論で初めて登場した。
| |
| − | <!--The example {{nowrap|'''R''' → '''S'''<sup>1</sup>}} given above is a universal cover. The map {{nowrap|'''S'''<sup>3</sup> → SO(3)}} from [[quaternion|unit quaternions]] to [[rotation]]s of 3D space described in [[quaternions and spatial rotation]] is also a universal cover.
| |
| − | | |
| − | If the space ''X'' carries some additional structure, then its universal cover usually inherits that structure:
| |
| − | * if the space ''X'' is a [[manifold]], then so is its universal cover ''D''
| |
| − | * if the space ''X'' is a [[Riemann surface]], then so is its universal cover ''D'', and ''p'' is a [[holomorphic]] map
| |
| − | * if the space ''X'' is a [[Lorentzian manifold]], then so is its universal cover. Furthermore, suppose the subset ''p''<sup>−1</sup>(''U'') is a [[disjoint union]] of open sets each of which is diffeomorphic with ''U'' by the mapping ''p''. If the space ''X'' contains a [[closed timelike curve]] (CTC), then the space ''X'' is [[timelike multiply connected]] (no CTC can be [[timelike homotopic]] to a point, as that point would not be causally well-behaved), its universal (diffeomorphic) cover is [[timelike simply connected]] (it does not contain a CTC).
| |
| − | * if ''X'' is a [[Lie group]] (as in the two examples above), then so is its universal cover ''D'', and the mapping ''p'' is a homomorphism of Lie groups. In this case the universal cover is also called the ''[[universal covering group]]''. This has particular application to [[representation theory]] and [[quantum mechanics]], since ordinary [[Group representation|representations]] of the universal covering group (''D'') are [[projective representation]]s of the original (classical) group (''X'').
| |
| − | | |
| − | The universal cover first arose in the theory of [[analytic functions]] as the natural domain of an [[analytic continuation]].-->
| |
| − | | |
| − | == G-被覆 ==
| |
| − | G を[[位相空間]] X 上の[[離散群]](discrete group)の[[群作用]]とする。どのような条件のときに X から[[群作用#軌道と等方部分群|軌道]] X/G への射影が被覆写像となるかとの問いは自然である。作用は不動点を持っているかもしれないので、これはいつの正しいとは限らない。例えば、{{nowrap|(x, y) ↦ (y, x)}} というツイスト作用により、積 {{nowrap|X × X}} 上への作用が、恒等元ではない位数 2 の巡回群が例である。このように X と X/G の基本群の間の関係の研究は、そうまっすぐには進めない。
| |
| − | | |
| − | しかしながら、群 G は X の基本グルーポイド(groupoid)上へ作用し、グルーポイド上への対応する群と対応する'''軌道'''を考えることで、最もうまく扱える。この理論は、以下の書籍 ''Topology and groupoids'' の第 11 章で定式化され、主要な結果は、普遍被覆を持つハウスドルフ空間 X 上の群 G の離散的作用に対し、軌道空間 X/G の基本グルーポイドは、X の基本グルーポイドの軌道グルーポイド、つまり、群 G の作用によるグルーポイドの商空間と同型ということである。これは計算を明確化し、例えば、空間の対称的な二乗積空間の基本群の計算に使われる。
| |
| − | <!--== G-coverings ==
| |
| − | Let ''G'' be a [[discrete group]] [[group action|acting]] on the [[topological space]] ''X''. It is natural to ask under what conditions the projection from ''X'' to the [[orbit space]] ''X''/''G'' is a covering map. This is not always true since the action may have fixed points. An example for this is the cyclic group of order 2 acting on a product {{nowrap|''X'' × ''X''}} by the twist action where the non-identity element acts by {{nowrap|(''x'', ''y'') ↦ (''y'', ''x'')}}. Thus the study of the relation between the fundamental groups of ''X'' and ''X''/''G'' is not so straightforward.
| |
| − | | |
| − | However the group ''G'' does act on the fundamental groupoid of ''X'', and so the study is best handled by considering groups acting on groupoids, and the corresponding ''orbit groupoids''. The theory for this is set down in Chapter 11 of the book ''Topology and groupoids'' referred to below. The main result is that for discontinuous actions of a group ''G'' on a Hausdorff space ''X'' which admits a universal cover, then the fundamental groupoid of the orbit space ''X''/''G'' is isomorphic to the orbit groupoid of the fundamental groupoid of ''X'', i.e. the quotient of that groupoid by the action of the group ''G''. This leads to explicit computations, for example of the fundamental group of the symmetric square of a space.-->
| |
| − | | |
| − | == 被覆変換 ==
| |
| − | 被覆 p : C → X の'''被覆変換'''、もしくは、'''自己同型'''とは、p ∘ f = p であるような C 上の[[同相写像|自己同相写像]] f : C → C のことを言う{{sfn|Bredon|1993|loc={{google books quote|id=G74V6UzL_PUC|page=147|Definition 6.1}}}}。被覆 p の被覆変換の全体は、[[写像の合成]]に関して群を成し、'''被覆変換群'''(covering transformation group) Aut(p) と呼ばれる。'''被覆変換'''(covering transformations)は'''デック変換'''(deck transformation)とも呼ばれる。全ての被覆変換は、各々のファイバーの元を[[置換 (数学)|置き換え]]る。このことは、各々のファイバー上で被覆変換の[[群作用]]を定義する。リフト(持ち上げ)の一意性により、f が恒等写像でなく C が弧状連結であれば、f は[[不動点]]を持たない。
| |
| − | <!--== {{anchor|Deck transformation}} Deck transformation group, regular covers ==
| |
| − | A '''deck transformation''' or '''automorphism''' of a cover {{nowrap|''p'' : ''C'' → ''X''}} is a [[homeomorphism]] {{nowrap|''f'' : ''C'' → ''C''}} such that {{nowrap|1=''p'' ∘ ''f'' = ''p''}}. The set of all deck transformations of ''p'' forms a group under [[function composition|composition]], the '''deck transformation group''' Aut(''p''). Deck transformations are also called '''covering transformations'''. Every deck transformation [[permutation|permutes]] the elements of each fiber. This defines a [[group action]] of the deck transformation group on each fiber. Note that by the unique lifting property, if ''f'' is not the identity and ''C'' is path connected, then ''f'' has no [[fixed point (mathematics)|fixed points]].-->
| |
| − | | |
| − | ここで、p : C → X が被覆写像で、C が連結かつ局所弧状連結であるとする(従って、X もそのようになる)。各々のファイバーの上での Aut(p) の作用は、[[群作用#作用の種類|自由]]である。この作用があるファイバー上で[[群作用#作用の種類|推移的]]であれば、すべてのファイバー上で推移的であり、この場合を被覆は'''正規'''(regular)や'''正則'''(normal)、'''ガロア的'''と呼ばれる。全てのそのような正規な被覆は、[[主バンドル|主 G-バンドル]]であり、G = Aut(p) は離散位相群と考えられる。
| |
| − | | |
| − | 全ての普遍被覆 p : D → X は正規であり、被覆変換群は[[基本群]] π<sub>1</sub>(X) に同型である。
| |
| − | | |
| − | 上記の p(z) = z<sup>n</sup> の例 p : '''C'''<sup>×</sup> → '''C'''<sup>×</sup> は、正規被覆であり、被覆変換は [[1の冪根|1の n-乗根]]による乗法であり、従って、被覆変換群は[[巡回群]] C<sub>n</sub> に同型である。
| |
| − | | |
| − | 他の例として、上記の p(z) = z<sup>n!</sup> の例 p : '''C'''* → '''C'''* も正規被覆であり、変換群の階層を持っている。実際、C<sub>x!</sub> は、1 ≤ x ≤ y ≤ n に対し C<sub>y!</sub> の部分群である。
| |
| − | <!--Now suppose {{nowrap|''p'' : ''C'' → ''X''}} is a covering map and ''C'' (and therefore also ''X'') is connected and locally path connected. The action of Aut(''p'') on each fiber is [[group action|free]]. If this action is [[group action#Types of actions|transitive]] on some fiber, then it is transitive on all fibers, and we call the cover '''regular''' (or '''normal''' or '''Galois'''). Every such regular cover is a [[principal bundle|principal ''G''-bundle]], where {{nowrap|1=''G'' = Aut(''p'')}} is considered as a discrete topological group.
| |
| − | | |
| − | Every universal cover {{nowrap|''p'' : ''D'' → ''X''}} is regular, with deck transformation group being isomorphic to the [[fundamental group]] π<sub>1</sub>(''X'').
| |
| − | | |
| − | The example {{nowrap|''p'' : '''C'''<sup>×</sup> → '''C'''<sup>×</sup>}} with {{nowrap|1=''p''(''z'') = ''z''<sup>''n''</sup>}} from above is a regular cover. The deck transformations are multiplications with ''n''-th [[root of unity|roots of unity]] and the deck transformation group is therefore isomorphic to the [[cyclic group]] ''C''<sub>''n''</sub>.
| |
| − | | |
| − | Another example: {{nowrap|''p'' : '''C'''* → '''C'''*}} with {{nowrap|1=''p''(''z'') = ''z''<sup>''n''!</sup>}} from above is regular. Here one has a hierarchy of deck transformation groups. In fact ''C''<sub>''x''!</sub> is a subgroup of ''C''<sub>''y''!</sub>, for {{nowrap|1 ≤ ''x'' ≤ ''y'' ≤ ''n''}}.-->
| |
| − | | |
| − | == モノドロミー作用 ==
| |
| − | {{main|モノドロミー}}
| |
| − | 再び、{{nowrap|''p'' : ''C'' → ''X''}} を被覆写像とし、C (と、従って X も)連結で局所弧状連結であるとする。x が X の点で c が x 上のファイバーに属し(つまり、{{nowrap|1=p(c) = x}})、{{nowrap|γ : [0, 1] → X}} が {{nowrap|1=γ(0) = γ(1) = x}} である経路とすると、この経路は出発点を c にもつ C の一意の経路へ持ち上げることができる。この持ち上げられた経路の終点は、c である必要はないが、x 上のファイバーの中に属す必要がある。この終点は基本群 {{nowrap|π<sub>1</sub>(X, x)}} の中の γ のクラスにのみ依存することが判明している。この形で、x 上のファイバーに {{nowrap|π<sub>1</sub>(X, x)}} の右からの[[群作用]]を得る。これは'''モノドロミー作用'''(monodromy action)として知られている。
| |
| − | | |
| − | ファイバー上には 2つの作用が存在し、{{nowrap|x : Aut(p)}} は左側より作用し、{{nowrap|π<sub>1</sub>(X, x)}} は右側より作用する。これらの 2つの作用は次の意味で整合性を持っている。Aut(p) の中の全ての f と p<sup>−1</sup>(x) の中の全ての c と、{{nowrap|π<sub>1</sub>(X, x)}}の中の全ての γ に対して、
| |
| − | <math>f\cdot(c\cdot\gamma) = (f\cdot c)\cdot\gamma</math> となる。
| |
| − | | |
| − | p が普遍被覆であれば、Aut(p) は自然に {{nowrap|π<sub>1</sub>(X, x)}} の[[双対 (圏論)|双対]](dual)群と同一視できるので、{{nowrap|π<sub>1</sub>(X, x)}} の双対群の作用は、x 上のファイバー上への Aut(p) の作用に一致する。Aut(p) と {{nowrap|π<sub>1</sub>(X, x)}} とは、この場合は自然に同型となる(群はいつも自然に {{nowrap|g ↦ g<sup>−1</sup>)}} を通して、双対と同型となる)。
| |
| − | | |
| − | p が[[被覆空間#被覆変換|正規]]被覆であれば、Aut(p) は自然に {{nowrap|π<sub>1</sub>(''X'', ''x'')}} の商に同型である。
| |
| − | | |
| − | 一般に、(適切な空間に対しては、) Aut(p) は、{{nowrap|p<sub>*</sub>(π<sub>1</sub>(C, c))}} 上で {{nowrap|π<sub>1</sub>(X, x)}} の中で {{nowrap|p<sub>*</sub>(π<sub>1</sub>(C, c))}} の[[中心化群と正規化群|正規化]]による商と、自然に同型となり、そこでは {{nowrap|1=p(c) = x}} となる。
| |
| − | <!--== Monodromy action ==
| |
| − | {{main|Monodromy}}
| |
| − | Again suppose {{nowrap|''p'' : ''C'' → ''X''}} is a covering map and ''C'' (and therefore also ''X'') is connected and locally path connected. If ''x'' is in ''X'' and ''c'' belongs to the fiber over ''x'' (i.e. {{nowrap|1=''p''(''c'') = ''x''}}), and {{nowrap|γ : [0, 1] → ''X''}} is a path with {{nowrap|1=γ(0) = γ(1) = ''x''}}, then this path lifts to a unique path in ''C'' with starting point ''c''. The end point of this lifted path need not be ''c'', but it must lie in the fiber over ''x''. It turns out that this end point only depends on the class of γ in the fundamental group {{nowrap|π<sub>1</sub>(''X'', ''x'')}}. In this fashion we obtain a right [[group action]] of {{nowrap|π<sub>1</sub>(''X'', ''x'')}} on the fiber over ''x''. This is known as the '''monodromy action'''.
| |
| − | | |
| − | There are two actions on the fiber over {{nowrap|''x'' : Aut(''p'')}} acts on the left and {{nowrap|π<sub>1</sub>(''X'', ''x'')}} acts on the right. These two actions are compatible in the following sense:
| |
| − | <math>f\cdot(c\cdot\gamma) = (f\cdot c)\cdot\gamma</math> for all ''f'' in Aut(''p''), ''c'' in ''p''<sup>−1</sup>(''x'') and γ in {{nowrap|π<sub>1</sub>(''X'', ''x'')}}.
| |
| − | | |
| − | If ''p'' is a universal cover, then Aut(''p'') can be naturally identified with the [[Dual (category theory)|opposite]] group of {{nowrap|π<sub>1</sub>(''X'', ''x'')}} so that the left action of the opposite group of {{nowrap|π<sub>1</sub>(''X'', ''x'')}} coincides with the action of Aut(''p'') on the fiber over ''x''. Note that Aut(''p'') and {{nowrap|π<sub>1</sub>(''X'', ''x'')}} are naturally isomorphic in this case (as a group is always naturally isomorphic to its opposite through {{nowrap|''g'' ↦ ''g''<sup>−1</sup>)}}.
| |
| − | | |
| − | If ''p'' is a [[Covering_space#Deck_transformation_group.2C_regular_covers|regular]] cover, then Aut(''p'') is naturally isomorphic to a quotient of {{nowrap|π<sub>1</sub>(''X'', ''x'')}}.
| |
| − | | |
| − | In general (for good spaces), Aut(''p'') is naturally isomorphic to the quotient of the [[Centralizer and normalizer|normalizer]] of {{nowrap|''p''<sub>*</sub>(π<sub>1</sub>(''C'', ''c''))}} in {{nowrap|π<sub>1</sub>(''X'', ''x'')}} over {{nowrap|''p''<sub>*</sub>(π<sub>1</sub>(''C'', ''c''))}}, where {{nowrap|1=''p''(''c'') = ''x''}}.-->
| |
| − | | |
| − | ==分類空間や群コホモロジーとの関係==
| |
| − | X を任意の n ≥ 2 に対する[[ホモトピー群]] π<sub>n</sub>(X) = 0 と持つ連結な{{仮リンク|胞体複体|en|cell complex}}(cell complex)とすると、X の普遍被覆空間 T は次のように{{仮リンク|ホワイトヘッドの定理|en|Whitehead theorem}}(Whitehead theorem)を適用すると、可縮であることが分かる。この場合に X は[[分類空間]]であり、G = π<sub>1</sub>(X) に対し K(G, 1) である。
| |
| − | | |
| − | さらに、すべての n ≥ 0 に対し、胞体 n-鎖体 C<sub>n</sub>(T) (つまり、n-胞体により T の中に与えられる基底をもつ[[自由アーベル群]])は、自然に '''Z'''G-[[加群 (数学)|加群]]構造をも持つ。ここに T の n-胞体 σ と G の元 g に対し、胞体 gσ は、正確に g に対応する T の被覆変化による σ の変換に一致する。さらに、C<sub>n</sub>(T) は、T の n-胞対の G-軌道の表現による自由 '''Z'''G-基底をもつ[[自由加群|自由]] '''Z'''G-加群である。この場合は、ε を{{仮リンク|アーギュメント写像|en|augmentation map}}(augmentation map)として、標準的なトポロジカルな鎖複体
| |
| − | | |
| − | :<math> \cdots \overset{\partial}{\to} C_n(T)\overset{\partial}{\to} C_{n-1}(T)\overset{\partial}{\to} \cdots \overset{\partial}{\to} C_0(T)\overset{\varepsilon}{\to} \mathbf Z </math>
| |
| − | | |
| − | は、'''Z''' の[[自由分解|自由 '''Z'''G-分解]](free '''Z'''''G''-resolution)である(ここの '''Z''' は、自明な '''Z'''G-加群構造を持ち、すべての g ∈ G とすべての m ∈ '''Z''' に対し gm = m となる)。この分解は任意の係数を持つ G の[[群コホモロジー]](group cohomology)の計算に使うことができる。
| |
| − | | |
| − | 群の分解を計算したりホモロジー代数の別の計算をするグラハム・エリス(Graham Ellis)の方法は、J. Symbolic Comp. の彼の論文や以下にあげるウェブページに示されているように、普遍被覆の収縮するホモトピーとして、同時に帰納的に K(G) の普遍被覆を構成する方法である。この後者が、計算可能な方法を与えている。
| |
| − | <!--==Relations with classifying spaces and group cohomology==
| |
| − | If ''X'' is a connected [[cell complex]] with [[homotopy group]]s {{nowrap|1=π<sub>''n''</sub>(''X'') = 0}} for all {{nowrap|''n'' ≥ 2}}, then the universal covering space ''T'' of ''X'' is contractible, as follows from applying the [[Whitehead theorem]] to ''T''. In this case ''X'' is a [[classifying space]] or {{nowrap|''K''(''G'', 1)}} for {{nowrap|1=''G'' = π<sub>''1''</sub>(''X'')}}.
| |
| − | | |
| − | Moreover, for every {{nowrap|''n'' ≥ 0}} the group of cellular ''n''-chains ''C''<sub>''n''</sub>(''T'') (that is, a [[free abelian group]] with basis given by ''n''-cells in ''T'') also has a natural '''Z'''''G''-[[Module (mathematics)|module]] structure. Here for an ''n''-cell ''σ'' in ''T'' and for ''g'' in ''G'' the cell ''g'' σ is exactly the translate of σ by a covering transformation of ''T'' corresponding to ''g''. Moreover, ''C''<sub>''n''</sub>(''T'') is a [[Free module|free]] '''Z'''''G''-module with free '''Z'''''G''-basis given by representatives of ''G''-orbits of ''n''-cells in ''T''. In this case the standard topological chain complex
| |
| − | | |
| − | :<math> \cdots \overset{\partial}{\to} C_n(T)\overset{\partial}{\to} C_{n-1}(T)\overset{\partial}{\to} \cdots \overset{\partial}{\to} C_0(T)\overset{\varepsilon}{\to} \mathbf Z, </math>
| |
| − | | |
| − | where ε is the [[augmentation map]], is a [[free resolution|free '''Z'''''G''-resolution]] of '''Z''' (where '''Z''' is equipped with the trivial '''Z'''''G''-module structure, {{nowrap|1=''gm'' = ''m''}} for every {{nowrap|''g'' ∈ ''G''}} and every {{nowrap|''m'' ∈ '''Z'''}}). This resolution can be used to compute [[group cohomology]] of ''G'' with arbitrary coefficients.
| |
| − | | |
| − | The method of Graham Ellis for computing group resolutions and other aspects of homological algebra, as shown in his paper in J. Symbolic Comp. and his web page listed below, is to build a universal cover of a prospective {{nowrap|''K''(''G'', 1)}} inductively at the same time as a contracting homotopy of this universal cover. It is the latter which gives the computational method.-->
| |
| − | | |
| − | ==一般化==
| |
| − | ホモトピー論として、被覆空間の考えは、デック変換群が離散的である場合、あるいは同じことであるが、空間が[[局所連結空間]]の場合に、有益である。しかし、デック変換群は[[離散位相|離散的]]ではない[[位相群]]なので、問題が発生する。{{仮リンク|ハワイアンリング|en|Hawaiian earring}}(Hawaiian earring)のような、より複雑な空間を作る発展もあった。さらに詳細は、参考文献を参照。
| |
| − | | |
| − | これらの問題の多くは、ジェレミー・ズラザス(Jeremy Brazas)による'''半被覆'''(semicovering)の考えにより解決された(以下の参考文献中の論文を参照)。<!--Every covering map is a semicovering, but semicoverings satisfy the "2 out of 3" rule: given a composition {{nowrap|1=''h'' = ''fg''}} of maps of spaces, if two of the maps are semicoverings, then so also is the third. This rule does not hold for coverings, since the composition of covering maps need not be a covering map.
| |
| − | | |
| − | そのほかの一般化は、自由ではない群の作用である。ロス・ゲオゲーガンはRoss Geoghegan in his 1986 review (MR0760769) of two papers by M.A. Armstrong on the fundamental groups of [[orbit space]]s wrote: "These two papers show which parts of elementary covering space theory carry over from the free to the nonfree case. This is the kind of basic material that ought to have been in standard textbooks on fundamental groups for the last fifty years." 現在、以下に一覧とした「位相とグルーポイド」はそのような結果の単に基本的な教科書であるように思える。-->
| |
| − | <!--==Generalizations==
| |
| − | As a homotopy theory, the notion of covering spaces works well when the deck transformation group is discrete, or, equivalently, when the space is [[locally path-connected]]. However, when the deck transformation group is a [[topological group]] whose topology is not [[discrete topology|discrete]], difficulties arise. Some progress has been made for more complex spaces, such as the [[Hawaiian earring]]; see the references there for further information.
| |
| − | | |
| − | A number of these difficulties are resolved with the notion of ''semicovering'' due to Jeremy Brazas, see the paper cited below. Every covering map is a semicovering, but semicoverings satisfy the "2 out of 3" rule: given a composition {{nowrap|1=''h'' = ''fg''}} of maps of spaces, if two of the maps are semicoverings, then so also is the third. This rule does not hold for coverings, since the composition of covering maps need not be a covering map.
| |
| − | | |
| − | Another generalisation is to actions of a group which are not free. Ross Geoghegan in his 1986 review (MR0760769) of two papers by M.A. Armstrong on the fundamental groups of [[orbit space]]s wrote: "These two papers show which parts of elementary covering space theory carry over from the free to the nonfree case. This is the kind of basic material that ought to have been in standard textbooks on fundamental groups for the last fifty years." At present, "Topology and Groupoids" listed below seems to be the only basic topology text to cover such results.-->
| |
| − | | |
| − | == 脚注 ==
| |
| − | {{reflist|2}}
| |
| − | | |
| − | == 参考文献 ==
| |
| − | * {{cite book | 和書 | author=鈴木 晋一 | title=曲面の線形トポロジー<上>、<下> | year=1986 | publisher=槇書店 | isbn=4837505570 }}
| |
| − | * {{cite book | 洋書 | last=Bredon | first=Glen E. | title=Topology and Geometry | year=1993 | publisher=Springer-Verlag | isbn=0-387-97926-3 | url={{google books|G74V6UzL_PUC|plainurl=yes}} | mr=1224675 | zbl=0791.55001 | ref=harv }}
| |
| − | * {{cite book | last = Lickorish | first=W. B. Raymond | title = An Introduction to Knot Theory | year = 1997 | publisher=Springer-Verlag | url={{google books|PhHhw_kRvewC|plainurl=yes}} | isbn=0-387-98254-X | mr=1472978 | zbl=0886.57001 | ref=harv }}
| |
| − | * {{cite book | last=Munkres | first=James R. | title=Topology | year=2000 | publisher=Prentice Hall | isbn=0-13-181629-2 | edition=Second | ref=harv }}
| |
| − | | |
| − | == 関連項目 ==
| |
| − | * [[層 (数学)]]
| |
| − | * [[アーベル圏]]
| |
| − | | |
| − | == 外部リンク ==
| |
| − | *{{SpringerEOM
| |
| − | | title=Covering
| |
| − | | id=Covering&oldid=13627
| |
| − | | last=Chernavskii
| |
| − | | first=A.V.
| |
| − | }}
| |
| | | | |
| | + | {{テンプレート:20180815sk}} |
| | {{デフォルトソート:ひふくくうかん}} | | {{デフォルトソート:ひふくくうかん}} |
| | [[Category:幾何学]] | | [[Category:幾何学]] |
![]() をつくり,射影
をつくり,射影 ![]() で考える。この
で考える。この ![]() を X の被覆空間という。
を X の被覆空間という。