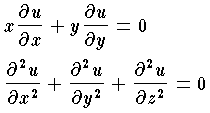|
|
| 1行目: |
1行目: |
| − | {{Differential equations}}
| + | '''偏微分方程式'''(へんびぶんほうていしき、{{lang-en-short|partial differential equation, '''PDE'''}}) |
| − | '''偏微分方程式'''(へんびぶんほうていしき、{{lang-en-short|partial differential equation, '''PDE'''}})は、未知関数の[[偏微分]]を含む[[微分方程式]]である。 | |
| | | | |
| − | == 概要 ==
| + | 未知関数が2個以上の変数の関数であって,未知関数のこれらに関する偏微分係数を含んでいる微分方程式を偏微分方程式という。たとえば,<i>u</i> を未知関数とすれば, |
| − | 微分方程式は通常多くの解を持ち、しばしば解集合を制限する[[境界条件]]を付加して考える。[[常微分方程式]]の場合にはそれぞれの解が幾つかの[[媒介変数|パラメータ]]の値によって特徴付けられるような族を解に持っているが、偏微分方程式については、パラメータは関数値をとると考えるほうが有用である(砕けた言い方をすれば、これは解の集合がとても大きいということである)。このことは、ひどく過剰決定的な方程式系でない限りかなり一般に正しい。
| |
| | | | |
| − | 偏微分方程式は、[[自然科学]]の分野で流体や[[重力場]]、[[電磁場]]といった[[場]]に関する自然現象を記述することにしばしば用いられる。これらの場というものは例えば、[[フライトシミュレーション]]や[[コンピュータグラフィックス]]、あるいは天気予報などといったものを扱うために重要な役割を果たす道具である。また、[[一般相対性理論]]や[[量子力学]]の基本的な方程式も偏微分方程式である。また、[[経済学]]においても重要な概念であり、特に金融工学において多用される。
| + | [[ファイル:10863000 siki1.gif|フレームなし|中央]] |
| | | | |
| − | == 記法 ==
| + | などは偏微分方程式である。 |
| − | 以下では未知関数 ψ の変数 ''x'' に関する偏微分を ψ<sub>''x''</sub> のように表す。
| |
| − | :<math>\psi_x := {\part \psi \over \part x},</math>
| |
| − | :<math>\psi_{xy} := {\part^2 \psi \over \part y\, \part x}.</math>
| |
| | | | |
| − | また、特別な記述がない限り、変数は[[時間]] ''t'' と[[3次元空間]] (''x'', ''y'', ''z'') とするが、数学的には一般の次元に拡張できる。
| |
| | | | |
| − | == 楕円型偏微分方程式 ==
| |
| − | {{main|楕円型偏微分方程式}}
| |
| − | === ラプラス方程式 ===
| |
| − | {{main|ラプラス方程式}}
| |
| − | 非常に重要で基礎的な偏微分方程式として、
| |
| − | : <math>\psi_{xx} + \psi_{yy} + \psi_{zz} = 0</math>
| |
| − | で定義される[[楕円型偏微分方程式]]を'''[[ラプラス方程式]]'''と呼ぶ。これはまた、∇([[ナブラ]])や Δ([[ラプラス作用素]])といった微分作用素を用いて
| |
| − | :<math>{\nabla}^2 \psi = 0, \quad \Delta \psi = 0</math>
| |
| − | のようにも書かれる。ラプラス方程式の解は'''[[調和関数]]'''と呼ばれ、重力場や[[静電場]]といった物理的な[[ベクトル場]]の[[ポテンシャル]]を与える。
| |
| − |
| |
| − | === ポアソン方程式 ===
| |
| − | {{main|ポアソン方程式}}
| |
| − | ラプラス方程式は既知の関数 ''f'' (''x'', ''y'', ''z'') に関する微分方程式
| |
| − | :<math>\nabla^2 \psi = \psi_{xx} + \psi_{yy} + \psi_{zz} = f(x,y,z)</math>
| |
| − | に一般化される。この偏微分方程式を'''[[ポアソン方程式]]'''という。これは質量の存在する重力場や、電荷の存在する静電場など、場に発生源がある場合のポテンシャルを記述する方程式である。
| |
| − |
| |
| − | === ヘルムホルツ方程式 ===
| |
| − | {{main|ヘルムホルツ方程式}}
| |
| − | 次の方程式のことをいう。[[電磁波]]の[[放射]]、[[地震学]]、[[音響学]]などで用いられる。
| |
| − | :<math>(\nabla^2 + k^2) \psi = 0</math>
| |
| − |
| |
| − | == 双曲型偏微分方程式 ==
| |
| − | {{main|双曲型偏微分方程式}}
| |
| − | === 波動方程式 ===
| |
| − | {{main|波動方程式}}
| |
| − | '''[[波動方程式]]'''は時間変数 ''t'' を含む[[双曲型偏微分方程式]]
| |
| − | : <math>\psi_{tt} = c^2 \nabla^2 \psi = c^2 (\psi_{xx} + \psi_{yy} + \psi_{zz})</math>
| |
| − | のことである。この方程式は[[光波]]や[[音波]]といった[[波]]を記述するもので、定数 ''c'' は波の速さを示している。より身近な現象として、[[ひも]]の振動であるとか[[太鼓]]の鼓面の振動などといったものもこの方程式に従う。波動方程式の解は基本的には[[正弦波]]を重ね合わせることによって得られる。
| |
| − |
| |
| − | === 移流方程式 ===
| |
| − | {{main|移流}}
| |
| − | '''[[移流]]方程式'''([[:en:Advection]])は速度場 '''u''' = (''u'', ''v'', ''w'' )のもとでの保存スカラー量ψの輸送を記述するもので、方程式は
| |
| − | :<math>\psi_t+\nabla\cdot(\bold{u}\psi) = \psi_t+(u\psi)_x+(v\psi)_y+(w\psi)_z = 0</math>
| |
| − | であたえられる。もし速度場 '''u''' が[[管状ベクトル場]]、すなわち ∇・'''u''' = 0 ならば方程式は
| |
| − | :<math>\psi_t+\bold{u}\cdot\nabla\psi = \psi_t+u\psi_x+v\psi_y+w\psi_z = 0</math>
| |
| − | と簡略化される。
| |
| − |
| |
| − | 一次元定常移流方程式
| |
| − | : <math>\psi_t + u\psi_x = 0</math>
| |
| − | (''u'' は定数)は一般に'''豚小屋問題''' (''pigpen problem'') と称される。
| |
| − |
| |
| − | == 放物型偏微分方程式 ==
| |
| − | {{main|放物型偏微分方程式}}
| |
| − | === 拡散方程式 ===
| |
| − | {{main|拡散方程式}}
| |
| − | '''[[拡散方程式]]'''は与えられた領域において時間とともに変化する場を記述する[[放物型偏微分方程式]]で、
| |
| − | :<math>u_t = k\nabla^2\psi = k (\psi_{xx} + \psi_{yy} + \psi_{zz})</math>
| |
| − | によって与えられる。ψはたとえば温度場([[熱伝導方程式]])や、物質の濃度場([[フィックの法則#フィックの第2法則|フィックの法則]])などを表す。定数 ''k'' は物質の熱伝導性や拡散係数などを示している。解は時間の増加とともに大体均一に分布するように変化し、''t''→∞で調和関数に近づく。
| |
| − |
| |
| − | === その他の方程式 ===
| |
| − | *[[シュレーディンガー方程式]]は[[量子力学]]の核心となる偏微分方程式である。
| |
| − |
| |
| − | == 非線型偏微分方程式 ==
| |
| − | 以上の例はすべて、 与えられた[[線形写像|線形作用素]] ''A'' と既知関数 ''f'' によって、''A''ψ = ''f'' という形に表されるという意味で[[線型方程式|線型]]である。 重要な非線型方程式には、
| |
| − | * 流体を記述する[[ナビエ-ストークス方程式]]
| |
| − | * [[一般相対性理論]]における[[アインシュタイン方程式|アインシュタインの場の方程式]]
| |
| − | * 非線形波動を記述する[[KdV方程式]]
| |
| − | *[[クレローの方程式]]
| |
| − | *[[非線形シュレディンガー方程式]]
| |
| − | などがある。
| |
| − |
| |
| − | == 解法 ==
| |
| − | 線型偏微分方程式は[[基底関数]]の集合で未知関数を展開することにより一般的に解かれる事が多い(たとえば[[正弦波]]関数を使った[[フーリエ級数]]展開)。展開した個々の解の[[線型結合]]がもとの方程式の解である。[[変数分離法]]はいくつかの重要な特別の応用をもつ。
| |
| − |
| |
| − | 非線型な微分方程式には一般に通用する解法というものは存在せず、実際に多くの微分方程式がまったく解析的には解くことが出来ない。しかしながら、いくつかのタイプの方程式には使える方法というのがある。たとえば、[[ホモトピー原理]]は過少決定性の方程式系を解くための非常に強力な方法である。
| |
| − |
| |
| − | ある場合には、偏微分方程式は解が、解の知られているある方程式の修正であると考えることで[[摂動]]解析によって解くことが出来る。別な方法として、単純な有限差分スキームから複雑な[[マルチグリッド法]]や[[有限要素法]]に至るまでの[[数値解析]]の手法が挙げられる。 科学や工学における多くの興味深い問題は高性能の[[スーパーコンピュータ]]を用いてこのような方法で解かれる。
| |
| − |
| |
| − | ''fill in: ''ディリクレ-ノイマン境界、双曲的/放物的/楕円的変数分離、[[フーリエ解析]]、[[グリーン関数]]
| |
| − |
| |
| − | == 関連項目 ==
| |
| − | {{commonscat|Partial differential equations}}
| |
| − | * [[楕円型偏微分方程式]]
| |
| − | * [[双曲型偏微分方程式]]
| |
| − | * [[放物型偏微分方程式]]
| |
| − | * [[常微分方程式]]
| |
| − | * [[積分方程式]]
| |
| − | * [[:en:Numerical partial differential equations]]
| |
| − |
| |
| − | == 参考文献 ==
| |
| − | {{参照方法|date=2016年1月}}
| |
| − | *{{Cite book|和書|author=寺沢寛一|authorlink=寺沢寛一|date=1983-05-18|title=自然科学者のための数学概論|edition=増訂版|publisher=岩波書店|isbn=4-00-005480-5}}
| |
| − | *{{Cite book|和書|author=溝畑茂|authorlink=溝畑茂|date=1965-08-25|title=偏微分方程式論|publisher=岩波書店|isbn=4-00-005971-8}}
| |
| − |
| |
| − | == 外部リンク ==
| |
| − | {{Spedia|Partial_differential_equation|Partial differential equation}}
| |
| − |
| |
| − | {{偏微分方程式の数値解法}}
| |
| | {{DEFAULTSORT:へんひふんほうていしき}} | | {{DEFAULTSORT:へんひふんほうていしき}} |
| | [[Category:微分方程式]] | | [[Category:微分方程式]] |
| | [[Category:偏微分方程式|*]] | | [[Category:偏微分方程式|*]] |
| | [[Category:数学に関する記事]] | | [[Category:数学に関する記事]] |