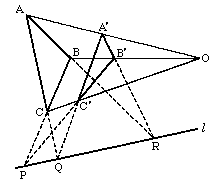
デザルグの定理
提供: miniwiki
デザルグの定理(デザルグの-ていり、théorème de Desargues)
デザルグの三角形定理ともいう。射影幾何学における最も基本的な定理。一つの平面上に,2つの三角形 ABC と A'B'C' があるとき,その対応する頂点をそれぞれ結んでできる直線 AA' ,BB' ,CC' が1点O で交わるならば,対応する辺 BC と B'C' ,CA と C'A' ,AB と A'B' のそれぞれの交点P ,Q ,R は1直線 l 上にある。この定理は,空間における2つの平行でない平面上の三角形についても成立する。このような関係におかれた2つの三角形を,配景の位置にあるデザルグの図形といい,O を配景の中心,l を配景の軸という。これらをまとめると,定理は「空間または同一平面上に,ある2つの三角形 ABC および A'B'C' があるならば,対応辺 BC と B'C' ,CA と C'A' ,AB と A'B' のそれぞれの交点は1直線上にある」と述べられる。 G.デザルグは,この定理において,BC と B'C' が平行な場合を取上げ,これら2直線は「無限遠点」で交わると述べている。3次元の場合は △ABC を含む平面と △A'B'C' を含む平面との交わりを考えれば簡単であるが,平面の場合は特別の意味をもち,一般の射影幾何としては,デザルグの定理の成り立たないような非デザルグ射影平面がある。